К
потолку лифта подвешен математический маятник, длина которого l. С каким ускорением и в каком
направлении должен двигаться лифт, что число колебаний возросло в 1,41 раза по
сравнению с колебаниями маятника в неподвижном лифте?
Решение.
Период
колебаний маятника в движущемся лифте зависит не только от ускорения свободного
падения, но и от ускорения движения лифта. Действительно, если лифт движется
ускорено, то F
= m(g + a).
Гармонические
колебаний маятника вызываются силой F
= -kx , k = mω2
– коэффициент квазиупрогуости, x
–
смещение. С другой стороны, F
= Fн sinα = Fнx/l (Fн – сила натяжения
подвеса маятника). Поэтому mω2x
= Fнx/l, откуда выражаем ω2 .
Так
как период колебаний T
= t/u , то совместным решением двух последний
уравнений найдем a.
Для движения лифта с ускорением, направленным против g.
Для
движения лифта с ускорением, совпадающем по направлению с ускорением силы
тяжести.
Для
того чтобы за одно и тоже время маятник совершил в 1,41 раза больше колебаний,
надо, чтобы период уменьшился в ^2 раз.
Это
возможно только в том случае, если a
= g и направлено противоположно
g, т.е. при ускоренном
подъеме или замедленном опускании с ускорением свободного падения. Если лифт
опускается ускоренно с ускорением g,
то T = ¥
, т.е. маятник покоится, так как находится в состоянии невесомости.
Важно
подчеркнуть, что с чем большей скоростью движется лифт, тем сильнее будут
отличаться период колебаний маятника от периода колебаний в покоящемся лифте.
Движение с постоянной скоростью не изменить периода при любой скорости
движения. В этом проявляется механический принцип относительности.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.


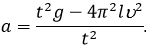


Комментариев нет:
Отправить комментарий