На горизонтальную стальную мембрану, совершающую вынужденные колебания с частотой 400 Гц т амплитудой 0,1 мм, насыпан мелкий песок. При некоторой амплитуде колебаний мембраны песчинки начинают подскакивать. Определите кинетическую энергию песчинки массой 0,1 мг в момент ее отрыва от мембраны.
Решение.
Систему
отсчета свяжем с поверхностью Земли и будем считать ее инерциальной.
Начало
координат выберем в состоянии устойчивого равновесия мембраны, ось OX направим вертикально вверх. В качестве
физических систем будем поочередно рассматривать мембрану и находящуюся на ней
песчинки.
Допустим,
что мембрана совершает гармонические колебания, т.е. в качестве идеальной
модели физической системы «мембрана» рассмотрим гармонический осциллятор. Пусть
в начальный момент времени осциллятор находится в состоянии равновесия и начал
двигаться вверх. Уравнение колебаний (зависимость координаты от времени) имеет
следующий вид.
Проекция
скорости и ускорения осциллятора на ось соответственно равны.
Физическая
система «песчинка» является незамкнутой. Ее можно принять за материальную точку
и описать вторым законом Ньютона.
N –
реакция мембраны, m0
– масса песчинки. Если спроецировать векторные величины на ось OX с учетом того, что до отрыва песчинки ль
мембраны их ускорения одинаковы, получим в проекциях.
Таким
образом, выделенные физические системы могут быть описаны следующими
уравнениями.
В
момент отрыва песчинки от мембраны (t
= t1
) N = 0 , поэтому max = - mg , т.е. ax = -g. Пусть значения координаты и проекции
скорости песчинки в этот момент времени равны соответственно x1 и v1 . С учетом этого,
уравнения, соответствующие моменту отрыва песчинки будут иметь вид.
Принимая
во внимание, что sin22put1 + cos22put1 = 1, решая совместно второе и третье уравнения,
получим.
Следовательно
можем найти кинетическую энергию песчинки в момент отрыва от мембраны.
С
учетом того, что в любой инерциальной системе отсчета кинетическая энергия
песчинки E
³
0 , полученная формула является ответом задачи, если выражение, которое стоит в
скобках, не отрицательное, т.е., если частота и амплитуда колебаний
удовлетворяют неравенству.
Ответ: E = нДж.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.







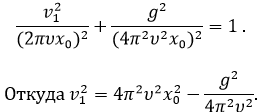


Комментариев нет:
Отправить комментарий