Составьте уравнение гармонических колебаний тела, если его максимальное ускорение равно по модулю 1,6 м/с2 , период колебаний 1 с, а смещение из состояния равновесия в начальный момент времени составляет 2 см.
Решение.
Будем
считать, что тело совершает гармонические колебания в инерциальной системе
отсчета после того, как его вывели и з состояния устойчивого равновесия, в
котором тело покоилось.
В качестве идеальной физической модели колеблющегося
тело выберем одномерный гармонический осциллятор. Начало координат выберем в
состоянии равновесия. Ось OX направим вдоль
направления движения тела. Тогда уравнение может быть записано в следующем
виде;
В
этой формуле x –
координата осциллятора в момент времени t,
ω –
циклическая частота, j0 – начальная фаза колебаний. Поскольку период колебаний
известен, то может найти ω.
Для
определения j0 используем начальные
условия. По условию задачи, при t = 0, x = x1 = 2 см, т.е. x1 = x0 sin j0 . Отсюда выражаем sinj0 .
Проекция
мгновенного ускорения осциллятора на ось OX имеет вид.
Поэтому
модуль его максимального значения равен a0 по модулю.
Откуда
можем найти амплитуду колебаний.
Таким
образом, начальная фаза колебаний и уравнение колебаний имеют вид.
После
подстановки числовых значений физических величин получим окончатальный ответ.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.



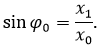
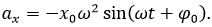



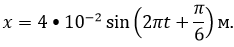
Комментариев нет:
Отправить комментарий