Три шарика, заряженные
равными одноименными зарядами q0 каждый, расположены в вершинах равностороннего треугольника со
стороной a. Определите напряженность и потенциал электростатического поля
в центре треугольника.
Решение.
Предположим, что шарики
покоятся относительно инерциальной системы отсчета, связанной с лабораторией.
В качестве физической
системы будем рассматривать три заряженных шарика. Если пренебречь
перераспределением зарядов шариков вследствие электростатической индукции, то
их заряды можно считать точечными. Для определения напряженности и потенциала
поля, созданного этими зарядами в центре треугольника, воспользуемся принципом
суперпозиции.
Укажем на схематическом
рисунке направления векторов E1 , E2 и E3 (считая заряды шариков
положительными). Начало координат выберем в центре треугольника, ось OY направим вертикально вниз, ось OX – горизонтально.
Проецируя векторы, изображающие напряженности на оси координат, получим систему
уравнений.
По условию задачи q1 = q2 = q3 = q0 . Расстояние
между центром треугольника и его вершинами равно r0 .
Следовательно, Ex =
0.
Так как α = p/6, то sinα = 1/2, т.е. Ey = 0. С учетом этого найдем модуль напряженности
электростатического поля в центре треугольника.
Если нулевой уровень
потенциала выбрать в бесконечности, то найдем потенциалы полей каждого заряда в
центре треугольника.
По принципу
суперпозиции потенциал поля в центре треугольника j.
Ответ: 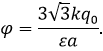 .
.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.

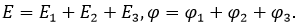






Комментариев нет:
Отправить комментарий