Как определить пройденный путь автомобиля при торможении?

Водитель выключил двигатель автомобиля и начал тормозить на горизонтальной дороге при скорости v0= 20 м/с. Определите путь, пройденный автомобилем за 15 с, если коэффициент трения при торможении равен 0,20.   

Решение.

 Систему  отсчета свяжем с поверхностью Земли и будем считать ее инерциальной. Начало координат выберем в точке, совпадающей с  положением центра масс автомобиля в момент времени t₀ = 0, что соответствует скорости v₀ = 20 м/с, ось OX направим вдоль движения, ось OY – вертикально вверх.

В физическую величину включим только автомобиль, который можно принять за материальную точку. Дорога, воздух и гравитационное поле Земли по отношению к выделенной системе являются внешними объектами. Взаимодействие системы с внешними объектами можно описать при помощи... соответствующих сил. Дорогу будем считать абсолютно твердым телом ( ее деформацией под действием автомобиля пренебрегаем, но упругие силы, возникающие при взаимодействии, необходимо учесть). На всем протяжении движения гравитационное поле Земли будем считать однородным и примем g = 10 м/с². Выталкивающую силу и силу сопротивления, действующие на автомобиль со стороны воздуха, во время движения учитывать не будем.

Анализ физической ситуации показывает, что на автомобиль действуют: сила тяжести mg, направленная вертикально вниз и обусловленная взаимодействием с гравитационным полем Земли; сила нормальной реакции дороги N, направленная вертикально вверх, и сила трения F_тр, направленная в сторону, противоположную движению, обусловлены взаимодействием дороги.

Согласно второму закону Ньютона: ma = mg + N + F_тр. Если спроецировать векторные величины на оси OX и OY, получим:    ma = F_тр, 0 = N – mg. 

Сила трения F_тр = µN. Поэтому ma = F_тр, N = mg, F_тр = µN, отсюда a = µg. Поскольку a = const, то движение автомобиля является равнопеременным. Поэтому кинематические законы его движения имеют вид:

                                        

или в скалярной форме:

                                        

 С учетом того, что a = µg, получим:

                                                   

Проанализируем полученные формулы. Спустя промежуток времени t₁ = 15 с после начала торможения проекция скорости на ось OX ( v_x = 20 – 30 = -10 м/с ) получается отрицательной, т.е. автомобиль должен двигаться в обратном направлении, но это запрещено условием задачи ( дорого горизонтальная, двигатель выключен). Таким образом, конечная скорость автомобиля должна быть равна нулю, а время его движения t₂ <15 с, т.е.

                                     

Решение последней системы уравнений относительно неизвестных дает:

                                          

Численно: l = 0.1 км, t₂ = 10 с.

   Заметим, что для нахождения l можно было воспользоваться не законами кинематики, а теоремой об изменении кинетической энергии автомобиля при торможении равно работе всех внешних сил, действующих на него, т.е. E = A.

                                        

                                        

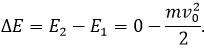
  ( работы силы тяжести и силы реакции дороги равны нулю), то

                                    

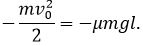
    Отсюда найдем l.

Источник:  Физика. Полный курс подготовки к ЦТ.   Под общей редакцией проф. В.А. Яковенко.