По наклонной к горизонту доске пустили катиться снизу вверх шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 с и через 2 с от начала движения. Определите начальную скорость и ускорение шарика, считая его постоянным.
Решение.
В качестве тела отсчета
выберем доску, ось OX
направим вдоль плоскости доски, начало координат выберем в точке начала
движения, отсчет времени начнем также с момента начала движения. При таком
выборе системы
отсчета x0 = 0, t0 = 0.
Движение шарика будем
считать прямолинейным, а по условию задачи его ускорение постоянно. Это значит,
что мы должны пренебречь взаимодействием шарика с воздухом, а поверхность доски
считать абсолютно гладкой. Поэтому кинематические законы движения шарика в
проекции на ось OX
имеют вид
Поскольку в моменты
времени t1 = 1 c и t2 = 2 с шарик находился в одной и той же точке доски, то его
координаты в эти моменты времени были одинаковыми, т.е. x1 = x2
= l. Таким образом
Решение этой системы
уравнений относительно v0 и a
приводит к результату
Правильность решения
можно проверить, например, путем сравнения наименований правой и левой частей
полученных формул или, исходя из энергетический соображений. Поскольку во время
движения шарика потери энергии отсутствуют, то его кинетическая энергия в
моменты времени t1 = 1 с и t2 = 2 с должна быть одинаковой. Для
проверки этого определим значения проекций скорости шарика на ось OX в эти моменты времени. Если подставить
значений v0 и a в формулы для vx и
v’x , получим:
Поскольку vx = | v’x |, то кинетическая энергия шарика в эти моменты времени
на самом деле одинакова, поэтому можно быть уверенным, что полученные значения v0 и a
являются решениями задачи в общем виде.
 28.2.13
28.2.13





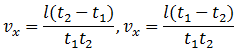







0 комментариев :
Отправить комментарий