Брусок
массой 1,5 кг удерживается в равновесии на гладкой плоскости тремя силами F1 , F2 и F3 , одна из которых направлена вертикально вверх, вторая – вверх
вдоль наклонной плоскости, третья – горизонтально под плоскость. Определите
силу реакции и угол наклона плоскости к горизонту, если модуль каждой из сил
равен 5 H.
Решение.
Систему
отсчета свяжем с поверхностью Земли и будем считать ее инерциальной. Начало
координат выберем в точке, совпадающей с центром масс бруска. Ось OX направим вниз вдоль наклонной плоскости,
ось OY
– перпендикулярно к
ней.
В
качестве физической системы рассмотрим брусок. Будем считать его материальной
точкой. Выделенная физическая система является незамкнутой. Ее взаимодействие с
внешними объектами можно описать при помощи соответствующих сил. Поскольку
выделенная физическая система относительно выбранной инерциальной системы
отсчета находится в равновесии, то геометрическая сумма сил, действующих на эту
систему, равна нулю.
Если
не учитывать взаимодействие бруска с воздухом, а силу трения покоя между ним и
наклонной плоскостью считать равной нулю, то на брусок действует сила тяжести mg , обусловленная его взаимодействием с
гравитационным полем Земли и направленная вертикально вниз, сила нормальной
реакции наклонной плоскости N
– направленная перпендикулярно
к плоскости, и заданные в условии задачи силы F1 , F2 и F3 .
В
соответствии с первым условием равновесия имеем.
Если
спроецировать векторные величины на оси координат получим систему уравнений.
С
учетом того, что F1 = F2 = F3 = 1/3 mg , получим окончательную систему.
Решение
этой системы относительно α и N
дает: α = 53°
, N = 10 H.
Ответ:
α = 53°
, N = 10 H.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 27.3.13
27.3.13



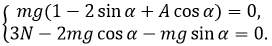







0 комментариев :
Отправить комментарий