При каком наименьшем угле наклона к горизонту лестница, приставленная к стене, будет находится в равновесии, если коэффициент трения между лестницей и полом равен µ1 , а между лестницей и стенкой µ2 ?
Решение.
Анализ
описанной в задаче физической ситуации показывает, что если в качестве
физической системы выбрать лестницу и считать ее абсолютно твердым телом,
находящимся в состоянии покоя в инерциальной системе отсчета, связанной с
поверхности Земли, то геометрическая сумма действующих на лестницу сил и
моментов этих сил относительно любой точки, лежащей в плоскости действия сил,
должны быть равными нулю.
Если
не учитывать выталкивающую силу со стороны воздуха, то на лестницу действует
сила тяжести mg,
приложенная в ее центре и направленная вертикально вниз, сила нормальной
реакции стены N2 , направленная горизонтально, сила
трения между лестницей и полом F1 , и сила трения покоя между лестницей и
стеной F2. Запишем первое условие равновесия.
Если
спроецировать векторные величины на оси OX и OY, то получим систему.
То
есть F1 = N2 , F2 = mg – N1 . С учетом того, что F1
≤ µ1N1 и F2 ≤ µ2N2
имеем.
Поскольку
в двух последних неравенствах имеются три неизвестных величины, составим в
явном виде уравнение моментов относительно точки соприкосновения лестницы с
полом (точка А).
В
этом уравнении l
– длинна лестницы, α –
угол наклона лестницы к горизонту. Если подставить в последнюю формулу значение
F2 = mg
– N1 получим новое уравнение.
С
учетом неравенств для N1 и
N2 получим.
Ответ  .
.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 31.3.13
31.3.13




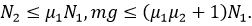

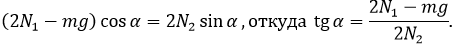
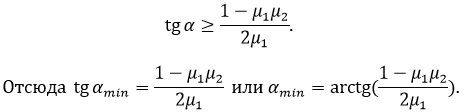







1 комментариев :
Спасибо огромное!
Благодаря вам всё понял!)
Отправить комментарий