Определите частоту вращения центрифуги радиусом 6 м, если вращение происходит в горизонтальной плоскости, а вес космонавта, массой 80 кг, находящегося в ней, равен 8 кН.
Решение.
Систему отсчета свяжем
с поверхностью Земли и будем считать ее инерциальной. Кроме того, будем
считать, что ось вращения центрифуги находится в состоянии покоя относительно
поверхности Земли.
В качестве физической
системы рассмотрим космонавта и примем его за материальную точку. Для решение
задачи применим законы кинематики движения материальной точки по окружности с
постоянной по модулю скоростью и законы динамики.
Если не учитывать
взаимодействие выделенной физической системы с воздухом, то космонавт,
находящийся в центрифуге, взаимодействует с гравитационным полем Земли, а также
сиденьем и спинкой кресла, т.е. на него действует сила тяжести mg и полная реакция кресла N, направленная под некоторым углом α к
вертикали.
Динамическое уравнение
движения космонавта имеет вид:
ma = mg + N.
Если
спроецировать векторные величины на оси OX и OY, получим:
Из
определения веса с учетом третьего закона Ньютона следует, что реакция кресла
численно равна весу космонавта, т.е. N
= P. Кроме того, an = 4π2n2r.
Таким
образом,
Если
решить последнюю систему уравнений относительно n, получим выражение.
После
подстановки числовых значений получим: n = 0.65 c-1.
Ответ:
n = 0.65 c-1.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 2.3.13
2.3.13


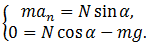

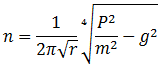







0 комментариев :
Отправить комментарий