Шар массой m, летящий горизонтально со скоростью v0 , сталкивается с неподвижной призмой массой M, стоящей на столе, и после абсолютно
упругого удара движется вертикально вверх. Определите максимальную высоту, на
которую поднимается шар, и расстояние, на которое переместится призма, если
коэффициент трения между ней и поверхностью стола равен μ.
Решение.
Систему отсчета свяжем
с поверхностью Земли и будем считать ее инерциальной.
Начало координат выберем в точке столкновения. Ось OX направим горизонтально, ось OY – вертикально вверх.
Начало координат выберем в точке столкновения. Ось OX направим горизонтально, ось OY – вертикально вверх.
Высоту поднятия шара и
перемещение призмы можно определить, если известны их скорости v1 и v2
в конце столкновения.
Для определения этих
скоростей рассмотрим физическую систему «шар - призма». Можно выделить два
состояния этой системы: начало о конец столкновения. Будем считать, что при
столкновении взаимодействия шара с призмой и призмы с поверхностью стола
происходят мгновенно и одновременно. Фактически это означает, что мы будем
рассматривать столкновение шара с системой «призма – поверхность стола».
Отметим, что допущение об одновременности и мгновенности взаимодействия
выполняется, если жесткость материала призмы больше и сравнима с жесткостью
материала шара, а их размеры также сравнимы между собой.
Поскольку выделенная
физическая система взаимодействует с материальными объектами, не входящими в
нее, то она является незамкнутой. Если не учитывать взаимодействие с воздухом,
то по горизонтали на физическую систему внешние силы не действуют.
Поэтому проекция полного импульса системы
на это направление сохраняется, т.е. (p1)x
= (p2)x , где
p1
= mv0 , p2
= mv1 + Mv2 .
Если спроецировать
векторные величины на ось OX,
получим: mv0
= Mv2 .
По условию задачи
рассматриваемая система консервативная, поэтому при переходе из начального
состояния в конечное в ней выполняется закон сохранения механической энергии.
Таким образом система «шар
– призма» математически описывается следующей системой уравнений.
Решение этой системы
дает скорости v1 и v2 ,
где v1 – скорость шара, v2
– скорость призмы сразу после столкновения.
Для определения
максимальной высоты, на которую поднимается шар, рассмотрим физическую систему «шар
после удара – гравитационное поле Земли». Можно выделить два состояния этой
систем: начальное – непосредственно после столкновения и конечное – в момент
времени, когда шар достиг максимальной высоты. Если не учитывать взаимодействие
шара с воздухом, то рассматриваемая физическая система является замкнутой и
консервативной и может быть описана законом сохранения механической энергии.
Если нулевой уровень
потенциальной энергии системы выбрать на горизонтали, проходящей через точку
столкновения, то начальная энергия системы E1 будет равна.
В конечном состоянии E2
.
Заметим, что полученная
формула является решением задачи при условии, если m/M < 1.
Если в физическую
систему включить только «шар после удара», то получим незамкнутую физическую
систему, которая может быть описана законами кинематики и динамики или теоремой
об изменении кинетической энергии.
В первом случает (если
не учитывать взаимодействие с воздухом) физическая система может быть описана
следующими законами.
Если перейти к
скалярной форме и учесть, что в верхней точке скорость шара равна нулю, получим
максимальную высоту поднятия шара.
При использовании
энергетического подхода ∆Ek
= A , где A – работа силы тяжести.
Таким образом,
независимо от выбора физической системы и законом, описывающих ее, получается
одно и тоже выражение для максимальной высоты подъема шара, хотя физическое
обоснование в этих случаях разное. Это свидетельствует о том, что высота, на
которую поднялся шар после столкновения, найдена правильно.
Для определения
перемещения призмы рассмотрим физическую систему «призма после столкновения».
Можно выделить два состояния этой системы: начальное – непосредственно после
столкновения и конечное – в момент
остановки призмы.
Выделенная физическая
система является незамкнутой, т.к. на нее действуют: сила тяжести Mg , обусловленная взаимодействием с
гравитационным полем Земли, сила реакции N и сила трения Fтр , обусловленные взаимодействием с поверхностью стола (взаимодействие
призмы с воздухом не учитываем).
Таким образом, про кинематико-динамическом подходе система может быть описана следующими законами.
Таким образом, про кинематико-динамическом подходе система может быть описана следующими законами.
Если перейти к
скалярной форме и учесть, что Fтр = μN
, в скорость призмы в конце движения v
= 0, получим l.
Можно использовать для
описания этой физической системы энергетический подход.
Работа силы тяжести и
силы реакции опоры равны нулю, поэтому работа внешних сил A = Aтр = Fтр cos180° = -μMgl. C учетом того, что v2 =
(mv0)/M найдем
l.
Совпадение
результатов свидетельствует о правильности решения задачи.
Ответ: 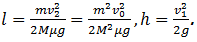 .
.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 16.3.13
16.3.13



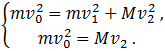
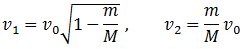
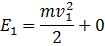

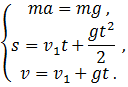













0 комментариев :
Отправить комментарий