Два тела массами m1 = 8 кг и m2
= 16 кг, связанные
невесомой нерастяжимой нитью, скользят по наклонной плоскости с углом наклона
300. Коэффициенты трения между телами и плоскостью равны μ1 = 0,25 и μ2 = 0,5. Определите ускорение тел и силу
натяжения нити.
Решение.
Движущиеся тела m1 и m2 взаимодействуют с гравитационной полем
Земли, т.е. на них действует силы тяжести m1g и m2g соответственно, направление вертикально
вниз; взаимодействие с наклонной плоскостью дает по две силы, действующие на
каждое из каждых тел, а именно: силы трения F1 и F2 , направленные по касательной вдоль
плоскости соприкосновения в сторону, противоположную движению, и силы реакции
наклонной плоскости N1 и N2 ; взаимодействие тел с нитью дает силы натяжения нити T1 и T2 .
Согласно второму закону
Ньютона
Если спроецировать
векторные величины на оси координат, получим
С учетом того, что нить
невесомая и нерастяжимая, имеем: T1
= T2 = T,
a1 = a2 = a3 , кроме того: F1 = μ1N1 , F2 = μ2N2 . Решение последней системы уравнения относительно неизвестных
дает:
После подстановки
числовых значений получим: a
= 1.4 м/с2 , T
= 12 Н.
Ответ: a = 1.4 м/с2 , T = 12 Н.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 3.3.13
3.3.13


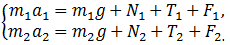
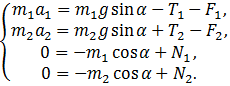








0 комментариев :
Отправить комментарий