Уравнение движения материальной точки массой 5 г имеет вид: x = 4sin(2pt/8 + 2). Определить амплитуду колебаний, начальную фазу, максимальную скорость, максимальное ускорение, максимальную силу, поддерживающую это движение, и полную энергию колеблющейся точки.
Решение.
Из аналогии данного в
условии задачи уравнения и уравнения гармонических колебаний следует, что
амплитуда колебаний x0
= 4 см;
циклическая частота ω=
2p/8
= p/4
с-1 ; начальная фаза j0
= 2 рад; скорость точки v
= x0ωcos(ωt + j0);
период колебаний T
= 2p/ω
= 8 с.
Максимальная скорость
будет в том случае, когда фаза ωt
+ j0
=
0, а cos(ωt + j0)
= 1; таким образом, v0
= x0ω
= 3,14 см/с. Скорость точки будет максимальной в положении равновесия.
Ускорение
точки a = -x0ω2sin(ωt + j0)
будет максимальный при фазе ωt
+ j0
= p/2
. В этом случае sin(ωt + j0)
= 1 и a0
= -x0ω2 = -2.5 см/с2
. Ускорение будет максимальным в крайних точках (максимально удаленных от
положения равновесия). Знак минус указывает на то, что ускорение всегда
направлено в сторону, противоположную смещению точки. Максимальную силу,
действующую на точку, найдем по второму закону Ньютона: F0 = ma0
= 1.25 мкH.
Полная
энергия точки имеет следующий вид.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 20.4.13
20.4.13

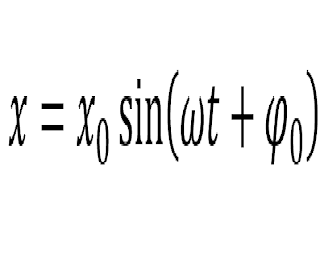








0 комментариев :
Отправить комментарий