Электрон влетает в пространство между обкладками плоского воздушного конденсатора под α к нижней обкладке. Определите минимальное значение модуля скорости электрона, при которой он достигнет верхней обкладки конденсатора, если напряжение между обкладками 60 В.
Решение.
Предположим, что
обкладки конденсатора покоятся относительно инерциальной системы отсчета,
связанной с лабораторией, и расположены горизонтально. Ось OX направим вдоль нижней обкладки конденсатора, ось OY –
вертикально вверх. Отсчет времени начнем в момент влета электрона в пространство
между обкладками конденсатора.
В качестве физической
системы рассмотрим «электрон». Будем считать его материальной точкой.
Выделенная система не замкнута, поэтому для решения задачи воспользуемся
кинематико-динамическим способом описания.
Движущийся в
пространстве между обкладками конденсатора электрон взаимодействует с
электростатическим полем конденсатора, с гравитационным и магнитным полями
Земли и с воздухом. Взаимодействие электрона с электростатическим полем можно
описать силой Fэл = eE, модуль которой, если пренебречь краевыми эффектами и явлением
электростатической индукции, не изменяется. Эта сила направлена против поля
(заряд электрона отрицательный). Взаимодействие электрона с гравитационным
полем Земли можно описать силой тяжести mg.
Если взаимодействием с воздухом и с магнитным полем пренебречь, то динамическое
уравнение движения электрона имеет вид: ma
= mg + eE. Принимая во внимание, что Fэл >> mg , получим ma = eE, т.е. движение электрона будет равноускоренным. Поэтому
кинематические законы движения электрона имеют следующий вид.
Проецируем векторы,
изображающее соответствующие величины, на оси координат.
Решив данную систему
уравнений относительно v0 , с учетом того, что E
= U/d, где d
– расстояние между обкладками
конденсатора, получим v0 .
Так как все величины,
входящие в формулу, за исключением vy
, постоянны, то v0 = f(vy). Вертикальная составляющая скорости электрона у верхней
обкладки должна удовлетворять условию vy
>= 0, т.е. в противном случае электрон
повернет обратно, так и не долетев до нее. Поэтому скорость влета электрона в
конденсатор будет минимальной, если vy
= 0.
Задачу можно решить,
применив к рассматриваемой физической системы теорему об изменении кинетической
энергии, согласно которой изменение кинетической энергии электрона при перемещений
из начального состояния в конечное в электростатическом поле конденсатора равно
работе внешних сил, действовавших на него во время движения. При сделанных допущениях
DWкин = Aэл.поля . если в качестве
начального состояния физической системы выбрать состояние в момент влета
электрона в конденсатор, а в качестве конечного – момент подлета к верхней
обкладки, то получаем.
Работа сил
электростатического поля A = -eU.
Так как vy >= 0, то получаем такую же самую формулу как и в первом
случае.
Этот же результат можно
получить, рассмотрев физическую систему «электрон – электрической поле
конденсатора», которая, если пренебречь взаимодействием с внешними объектами,
является замкнутой и может быть описана
законом сохранений энергии, в соответствии с которым энергия системы в момент
влета электрона в конденсатор равна ее энергии в тот момент времени, когда
электрон окажется у верхней обкладки.
Выбираем нулевой
уровень потенциала на верхней обкладке конденсатора.
Где eU –
потенциальная энергия взаимодействия электрона с электростатическим полем
конденсатора. Энергия системы в конечном состоянии – Wкон .
Таким образом,
использование различных вариантов теоретического базиса решения задачи и
различный выбор физических систем приводят к одному и тому же результату, что
свидетельствует о правильности ее решения.
Заметим, что полученное
значение v0min
является ответом задачи при условии, что
угол α удовлетворяет условию α >= arctg 2d/l.
Ответ: 
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 15.6.13
15.6.13


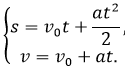


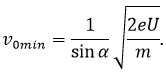
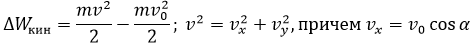
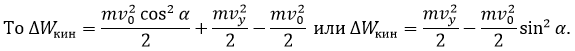











0 комментариев :
Отправить комментарий