В однородном
вертикальном электростатическом поле, напряженность которого E, на нити длиной l подвешен шарик массой m и зарядом q. Какую минимальную
скорость нужно сообщить шарику, чтобы он сделал полный оборот в вертикальной
плоскости?
Решение.
В качестве физической
системы рассмотрим заряженный шарик, который примем за материальную точку, а
его заряд будем считать точечным. Выделенная физическая система является
незамкнутой и следовательно, может быть описана законами кинематики, динамики и
теоремой об изменении кинетической энергии.
В качестве начального
выберем состояние рассматриваемой системы в момент времени t0 = 0, когда шарику
сообщили искомую скорость v0 , в качестве конечного – состояние в момент времени, когда
шарик оказался в верхней точке траектории. Изменение кинетической энергии
шарика при переходе из начального состояния в конечное равно работе всех
внешних сил, действующих на него.
Если пренебречь
взаимодействием с воздухом, электрическим и магнитным полями Земли, то во время
движения на шарик действуют сила тяжести mg,
сила упругости нити Fупр и сила взаимодействия
с внешним электростатическим полем Fэл = qE.
Так как в любой точке
траектории сила упругости перпендикулярна к направлению движения шарика, то
работа этой силы при его перемещении из начального состояния в конечное равна
нулю. Поэтому DWкин = A1 + A2 , где A1 – работа силы тяжести,
A2 – работа силы
электростатического взаимодействия с внешним полем. С другой стороны DWкин = mv2/2 – mv02/2, где v
и v0 – модули скоростей шарика в верхней и нижней точках траектории
соответственно.
Работа в
электростатическом и гравитационном полях не зависит от формы траектории и
определяется только координатами шарика в начальный и конечный моменты времени.
Поэтому A1 = -2mgr , где r = l –
радиус окружности, по которой движется шарик. A2 = ±2qEr , причем знак «плюс» соответствует случаю, когда вектор
напряженности внешнего электростатического поля E
направлен вертикально вверх и заряд шарика положительный; или случаю, когда E направлен вертикально вниз и заряд шарика отрицательный. Таким
образом, A = -2mgr ± 2qEr. Подставляем значения DWкин и A в аналитическое выражение теоремы об изменении кинетической
энергии.
Для нахождения v воспользуемся вторым законом Ньютона, записав его для момента
времени, соответствующего верхней точки траектории. С учетом сделанных выше
допущений, ma = mg + Fупр + qE, где a
– полное ускорение шарика в этой точке.
Проецируя векторы, изображающие соответствующие величины, на ось OY, направленную вниз получим: maн = mg ± qE + Fупр , где a = v2/l –
центростремительное ускорение шарика в верхней точке траектории.
Так как все величины,
входящие в формулу, за исключением силы упругости, постоянны, то v0 = f(Fупр). Fупр >= 0.
Из формулы видно, что
если сила электростатического взаимодействия направлена вниз, то v0min
> 0 при любых числовых значениях величин, входящих в нее (подумайте, до
каких пор можно увеличить заряд шарика и поле; чем вызваны ограничения). Если
сила электростатического взаимодействия направлена вертикально вверх, то v0min
> 0, при условии, что qE < mg.
Ответ: 
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
 13.6.13
13.6.13




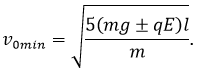







0 комментариев :
Отправить комментарий